LAS PROYECCIONES CARTOGRÁFICAS
Para representar la totalidad de la superficie terrestre sin ningún tipo de distorsión, un mapa debe tener una superficie esférica como la de un globo terráqueo. Como esta solución presenta numerosos problemas de manejo se han de realizar las proyecciones.
Para mostrar grandes porciones de la superficie o áreas de tamaño medio con precisión, la superficie esférica de la Tierra debe transformarse en una superficie plana. El sistema de transformación se denomina proyección.
Cuando una superficie esférica se transfiere a un plano modifica su geometría y la distorsiona, pero existen muchas transformaciones que mantienen una o varias de las propiedades geométricas del globo.
Dependiendo de la extensión y ubicación de la zona a representar en el plano o mapa, el cartógrafo elegirá un tipo de proyección u otro, teniendo en cuenta las características geométricas que cada uno de ellos conserva y las que no, así como los efectos que su uso tendrá en la representación de los ángulos, áreas, distancias y direcciones de la superficie a cartografiar; optará por alcanzar la precisión en uno de estos aspectos, en detrimento de la distorsión que se produzca en los restantes.
Una gran cantidad de mapas precisan más de una proyección cartográfica o, lo que es igual, una combinación de propiedades características de varias proyecciones (equivalencia, conformidad y acimut).
La clasificación de las proyecciones es compleja, pero normalmente se establece en función de la figura geométrica capaz de aplanarse que se elija para representar la tierra: un cono o un cilindro, que pueden cortarse y extenderse sobre una superficie plana, o un plano.
De este modo, clasificaremos las proyecciones en tres grupos fundamentales:
1) -acimutales (o planas).
2) -cónicas,
3) -cilíndricas
Otras clasificaciones tienen en cuenta el aspecto de la retícula y la relación de la superficie esférica con el plano (secante, tangente, transversal u oblicua); y otras se definen en función de su principal propiedad o atributo, hablando así de proyecciones conformes, equivalentes, equidistantes, etc.
1- Proyección plana o acimutal:
Se construye el mapa imaginando o situando un plano tangente o secante a un punto de la superficie de la Tierra. Son las más indicadas para representar superficies reducidas o cuando interesa que la información gravite en torno a u
n punto central.
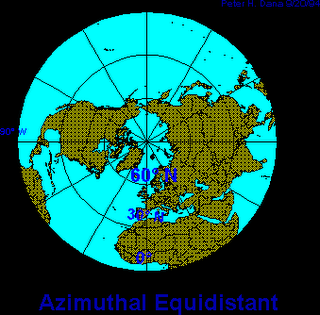
2- Proyección cónica:
Se obtiene el mapa imaginando un cono que envuelve a la esfera a la esfera terrestre. El cono enseguida se desenrolla sobre un plano. Las proyecciones cónicas pueden ser tangentes o secantes. Para preparar una proyección cónica debe colocarse un cono en el extremo superior del globo terráqueo. Tras la proyección, se supone que se corta el cono y se desarrolla hasta quedar como una superficie plana. El cono es tangente al globo en uno o varios paralelos base; el mapa que resulta de ello es muy preciso a lo largo de estos paralelos y áreas próximas, pero la distorsión aumenta progresivamente a medida que nos alejamos de ellos.
La proyección cónica conforme de Lambert, con dos paralelos base, se utiliza frecuentemente para cartografiar país
es o continentes pequeños como Australia o Europa .
es o continentes pequeños como Australia o Europa . En todas las proyecciones cónicas normales los meridianos son rectas que convergen en un punto (que representa el vértice del cono) y todos los paralelos son circunferencias concéntricas a ese punto.
3- Proyección cilíndrica:
Se obtiene el mapa imaginando un cilindro tangente o secante a la superficie de la Tierra. El cilindro es después desenrollado sobre un plano. Se usaban ya en el siglo XVI por el cartógrafo holandés Gerhard Kremer, que utilizaba el nombre latinizado de Mercator. La de Mercator es cilíndrica y conforme.
En todas las proyecciones cilíndricas normales los meridianos y los paralelos son representados por rectas perpendiculares.
Las proyecciones cilíndricas pueden ser:
Según la posición de la figura.
En este grupo son clasificadas las proyecciones por la inclinación del eje de la figura geométrica seleccionada . Si el eje es vertical, es decir orientado Norte- Sur, la proyección será normal, Ahora si el eje es horizontal con una orientación Este- Oeste, la proyección se de
nomina transversal. Cuando el eje se se dispone de manera diagonal, entonces la proyección será Oblicua.Transversal: para puntos situados en un mismo meridiano.
Longitudinales: para latitudes ecuatoriales
Oblicua: Representa un hemisferio como si se viera desde gran distancia.
LAS PROYECCIONES PUEDEN SER:
Proyecciones conformes: Las que representan la esfera respetando la forma, pero no el tamaño.
Ejemplo: La proyección de Mercator y la de Lambert
Proyecciones equivalentes: Las que respetan las dimensiones de las áreas pero no respetan sus formas.
Ejemplo: La proyección de Peters. (Hay distorsión también en las distancias).
Proyecciones equidistantes: Las que mantienen la distancia real entre los distintos puntos del mapa.
Ejemplo: la acimutal. Utilizada por los navegantes.
MAPAS RESULTANTES
Debido a que el punto de contacto entre la esfera y el plano es un punto sencillo, la distorsión del factor de escala será circularmente simétrica. Esto es, el factor de escala será proporcional a la distancia del centro de la proyección.
1) Las proyecciones acimutales :
a) el punto de tangencia es el centro de un mapa circular
b) todos los grandes círculos que pasan por el punto central son líneas rectas y todas las direcciones desde el punto central son exactas. Si el punto central es un polo, entonces los meridianos (los grandes círculos) radian desde ese punto y las paralelas se muestran como círculos concéntricos.
c) Una proyección azimutal es, por consiguiente, particularmente adecuada para rasgos 'circulares' pequeños sobre la superficie de la tierra. Por ejemplo: los polos o regiones pequeñas.
2) Cilíndrico transversal (secante):
2) Cilíndrico transversal (secante):
a) La proyección de Mercator permite introducir otra variante muy utilizada en cartografía: la proyección UTM (Universal Transversl de Mercator), una proyección cilíndrica transversal secante. Se basa en la proyección Mercator, en la que el cilindro es tangente a un meridiano; pero su "universalidad" se consigue empleando distintos cilindros tangentes a varios meridianos, separados entre sí 6º.
b) En cada proyección, sólo el meridiano de origen de cada huso de 6º y el ecuador aparecen como líneas rectas.
c) Las regiones que se encuentran por encima de los 80º de latitud no se suelen representar en la proyección UTM.
LAS DEFORMACIONES DE LAS PROYECCIONES
Ninguna proyección puede ser a la vez conforme y equiarea, pues entonces se tendría un mapa de distorsiones , lo que no es posible, como se demuestra en geometría diferencial.
Según la deformación que corrige.
Como la superficie de la Tierra es curva e irregular es imposible hacer una copia plana de esta superficie sin desfigurarla o alterarla. Por eso se debe escoger entre una posible conservación de los ángulos una proporcionalidad de las superficies o otro método que reduzca los efectos de la deformación, el cartógrafo debe saber cual de estas es más conveniente según los requerimientos del mapa.
· Conformes : Son aquellos donde no se distorsionan los ángulos
· Equivalentes o equiarea: Son aquellas en las cuales no se distorsionan las superficies Ejemplos: Cónica de Albers, Acimutal de Lambert.
· Equidistantes: Conservan la proporción entre las distancias, en determinadas direcciones, en la superficie representada. Ejemplo: Cilíndrica Equidistante.
· Proyecciones Afilacticas: Son aquellas que no son conformes , ni equiareas y que tratan de reducir al mínimo ambas alteraciones.
EJERCICIOS
1.-Comenta qué tipo de proyección utilizarías para:
-Representar Asia
-Para representar un país pequeño.
2.-Enumera las diferentes proyecciones y comenta sus características.
Página web muy completa sobre proyecciones. Es un documento científico de 102 páginas:
No hay comentarios:
Publicar un comentario